ENEM

Gabarito do Enem 2017 (Oficial) Será Publicado em 16 de Novembro O gabarito do Enem 2017 oficial será publicado em 16 de novembro, apenas quatro dias após a aplicação das provas de Ciências da Natureza e Matemática no dia 12, segundo domingo de realização do exame nacional. Nesta mesma data também serão liberadas as provas digitalizadas. O gabarito consiste na lista de respostas corretas para o conjunto de 45 questões que compõem cada uma das provas do objetivas do Enem, que além das duas áreas acima também conta com Linguagens e Códigos e Ciências Humanas, que serão realizadas em 2 de novembro. o Inep sempre faz a divulgação do gabarito em sua página oficial na internet, em arquivos no formato .pdf separados por dia de aplicação. Portanto, cada arquivo terá a lista de 90 alternativas corretas para cada dia, sendo 45 para cada prova objetiva. Vale lembrar, no entanto, que por questões de segurança o Enem traz cinco cores diferentes de cadernos de provas por dia de aplicação (azul, amarelo, rosa, branco e cinza), nos quais a lista de questões varia e consequentemente o gabarito também. Enem 2017 (5 de novembro) Gabarito Prova Amarela Gabarito Prova Azul Gabarito Prova Branca Gabarito Prova Rosa Enem 2017 (12 de novembro) Gabarito Prova Amarela Gabarito Prova Azul Gabarito Prova Cinza Gabarito Prova Rosa Note que, com exceção das provas branca e cinza, específicas ao primeiro e segundo dias, respectivamente, todas as outras cores de caderno (azul, amarela e rosa) estão presentes em ambos os dias. Vale esclarecer, no entanto, que não necessariamente o candidato resolverá, no segundo dia, caderno de cor equivalente ao primeiro. A distribuição dos cadernos é aleatória em relação ao candidato, respeitando somente o posicionamento da carteira em que ocupa no local de provas. Vale esclarecer ainda que com o gabarito em mãos o estudante poderá apenas saber a quantidade de itens acertados e errados no Enem 2017, sendo que a nota final não será equivalente ao total de questões respondidas corretamente. O que é Teoria de Resposta ao Item (TRI) Diferentemente das formas de correções tradicionais, nas quais apenas o total dos acertos é levado em conta, a Teoria de Resposta ao Item (TRI) releva também as habilidades exigidas do aluno e o nível de dificuldade de cada teste. Dessa forma, a TRI, utilizando funções e modelos matemáticos complexos, consegue estimar a probabilidade de cada participante responder acertadamente a determinada questão. Em outras palavras, por mais incrível que pareça, ela consegue identificar prováveis “chutes” de uma forma bastante precisa. No caso do Enem, o modelo utilizado foi desenvolvido em 1968 pelo matemático Birbaum. Nele, são avaliados três parâmetros: poder de discriminação, que diz respeito às habilidades dos alunos. a dificuldade de cada item (questão). a probabilidade de acerto ao acaso, popularmente chamado de “chute”. Como a TRI Consegue Descriminar um Chute? Antes de tudo, é importante ressaltar que todas as questões da prova são previamente testadas, com a finalidade de conhecer a dificuldade de cada uma delas. Com os dados coletados e com o modelo matemático de Birbaum, são construídas as curvas características de cada questão. 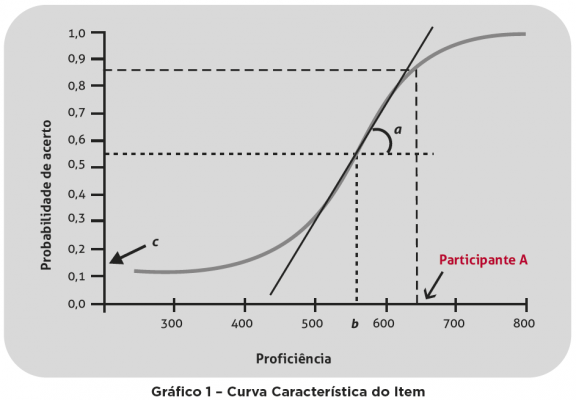Veja abaixo um exemplo desse dessa curva (gráfico 1): No exemplo acima, o suposto candidato A, que tem uma proficiência estimada de 650, teria aproximadamente 90% de chance de acertar a referida questão. Mas Como a TRI Define a Proficiência de Cada Candidato? Através do padrão de resposta de cada participante. Por exemplo, imagine uma prova com cinco questões com os seguintes enunciados: Questão 1 (Proficiência 300): Identifique, entre as figuras abaixo, qual delas é um cilindro. Questão 2 (Proficiência 400): Assinale a alternativa que representa corretamente a fórmula para calcular o volume de um cilindro. Questão 3 (Proficiência 500): Calcule o volume de combustível do cilindro ao lado. Questão 4 (Proficiência 600): O volume de um cilindro é de 60 dm³. Se o raio da base mede o dobro da altura, determine a altura do cilindro. Questão 5 (Proficiência 700): Considere um cilindro de raio r e altura h, cuja capacidade é V. Triplicando-se a altura e dobrando o raio, qual será seu novo volume? Antes de explicar como o modelo consegue estimar a proficiência de cada participante, vale ressaltar que nos exemplos acima não colocamos as alternativas, pois, neste momento, as mesmas são irrelevantes. Certamente você percebeu que as questões apresentam dificuldades (Proficiência) diferentes e crescentes. Ou seja, a primeira é a mais fácil de todas e a última a mais difícil. Com isso em mente, considere três alunos (a, b e c) e seus respectivos acertos descritos abaixo: A – Acertou 1, 2 e 3 B – Acertou 1, 2 e 4 C – Acertou 3, 4 e 5 Note que os três supostos participantes obtiveram três acertos cada. Ou seja, numa prova convencional, todos eles teriam a mesma nota. Entretanto, seja sincero! Qual dos três você gostaria de ter na sua universidade? Antes de responder, vamos analisar o padrão de acertos de cada um. O aluno A teve um padrão de resposta bastante coerente, pois quando se deparou com cinco questões sobre cilindro, ele acertou as três mais fáceis e errou as duas mais difíceis. Já o padrão de resposta do aluno B demonstra uma certa incoerência, afinal acertou a questão 4 e errou a questão 3, que é mais fácil. Quando analisamos as respostas do aluno C, a falta de coerência fica bastante evidente, pois das cinco questões sobre o mesmo assunto, ele acertou as três mais difíceis e errou as duas mais fáceis. Dessa forma, podemos supor que o modelo matemática designará as seguintes proficiência para cada aluno: Aluno A: 520 Aluno B: 480 Aluno C: 340 Agora voltamos a pergunta: qual deles você gostaria de ter na sua universidade? Tenho certeza que sua preferência será pelo aluno A. É importante ressaltar que este exemplo é apenas uma simplificação para tentar ilustrar a lógica que o modelo matemático utiliza para classificar a proficiência de cada participante. Conclusão Com a curva característica de cada questão e com o padrão de resposta de cada participante, é possível prever a chance de acerto ao acaso de todos participantes em todas as questões! Fantástico, não é?